Разноцветные точки
Рассмотрим точек на плоскости, пронумерованных от до , обозначим их как , координаты -й точки .
Рассмотрим следующий процесс. Выберем номер начальной точки и номер следующей за ней точки (), а также целое число . После этого номер прицельной точки вычисляется по следующему алгоритму. Рассмотрим вектор , направленный из точки в точку . Упорядочим все точки, кроме -й, по углу, отсчитывая против часовой стрелки от направления вектора, равного , отложенного из точки . При равенстве угла будем упорядочивать точки по возрастанию расстояния до точки . В качестве точки выбирается точка, являющаяся -й в данном порядке при нумерации с единицы. Далее точка становится начальной, а точка — следующей за ней, после чего, пользуясь тем же алгоритмом, вычисляется номер прицельной точки. Этот процесс повторяется до бесконечности.
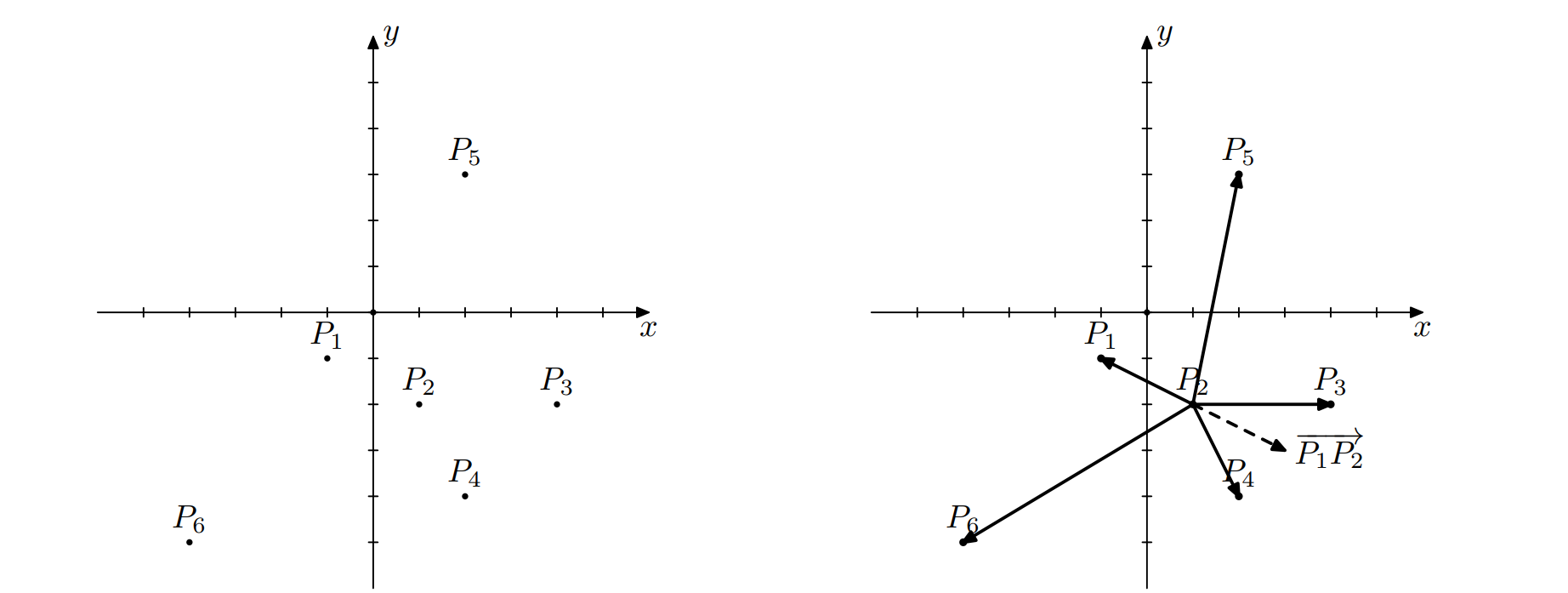
Для лучшего понимания процесса рассмотрим следующий пример. Пусть имеются точек, изображенных на рисунке , а . Пусть номер начальной точки равен , а номер следующей за ней точки равен . Отложим вектор от точки и отсортируем все точки, кроме точки , по углу, отсчитывая против часовой стрелки от направления данного вектора. На рисунке 2 отложенный вектор обозначен пунктирной линией, а также для удобства проведены векторы из точки во все остальные точки.
Рисунок 1: Пример множества из 6 точек.
Рисунок 2: Вектор , а также векторы из точки во все остальные точки.
Точки будут упорядочены следующим образом: . Таким образом, номер прицельной точки равен . Далее точка становится начальной, а точка — следующей.
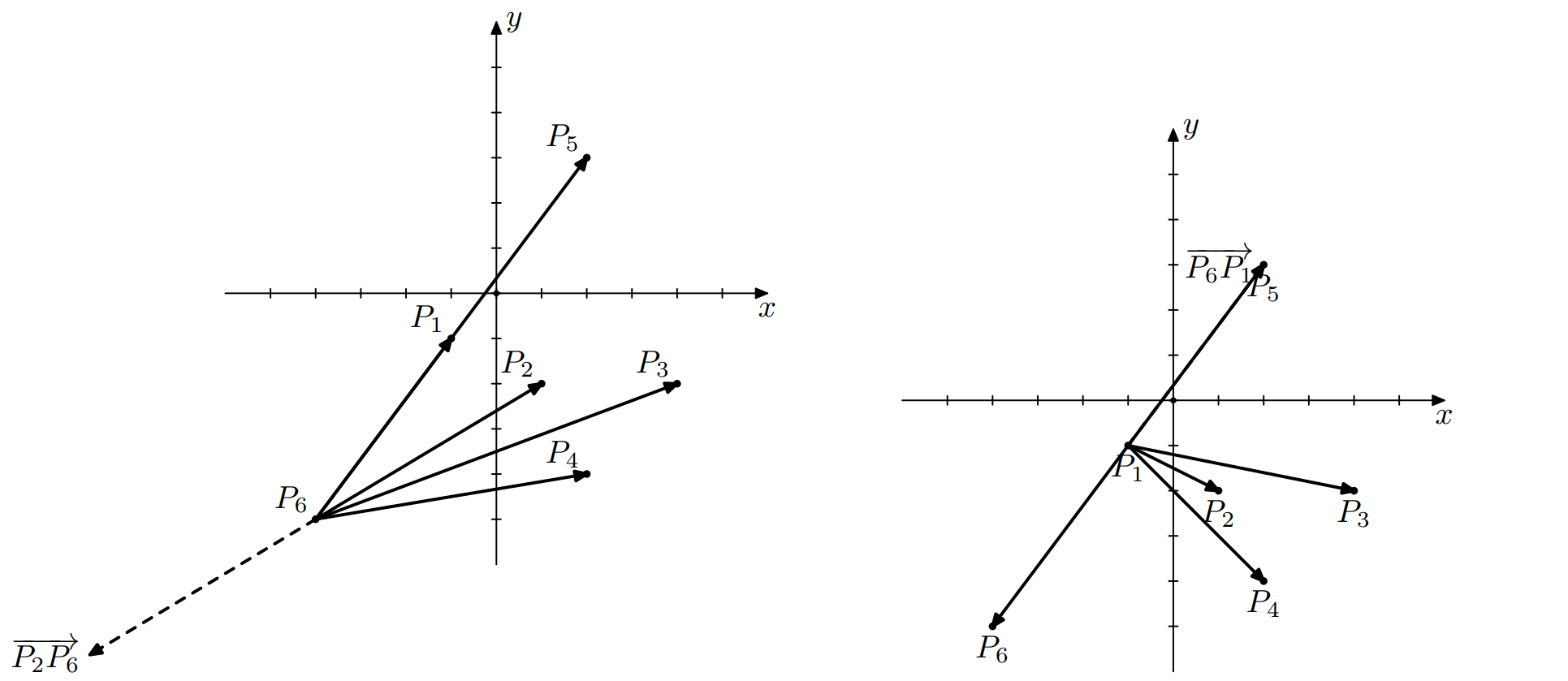
На рисунке 3 изображен процесс для начальной точки и следующей точки . Точки будут упорядочены следующим образом: . Обратите внимание, что точка в этом списке находится раньше, чем точка , так как расстояние от точки до точки меньше, чем расстояние от точки до точки . Прицельная точка будет иметь номер .
На рисунке 4 изображен процесс для начальной точки и следующей точки . Обратите внимание, что в данном случае вектор , отложенный из точки совпадает с вектором , отложенным из точки . Эти векторы изображены сплошной линией. Точки будут упорядочены следующим образом: . Прицельная точка будет иметь номер . Таким образом, далее процесс начнется для начальной точки и следующей точки и зациклится:
Покрасим каждую из точек в один из трех цветов. Цвет -й точки определяется следующим образом:
- Пусть существует такая точка , что, выбрав точку в качестве начальной, а точку в качестве следующей, в результате описанного процесса точка побывает начальной бесконечное количество раз. В этом случае точка будет покрашена в зеленый цвет.
- Пусть точка не была покрашена в зеленый цвет и существует такая точка , что, выбрав точку в качестве начальной, а точку в качестве следующей, в результате описанного процесса точка побывает начальной еще хотя бы один раз. В этом случае точка будет покрашена в синий цвет.
- Пусть точка не была покрашена ни в зеленый, ни в синий цвет. В этом случае точка будет покрашена в красный цвет.
Для каждой точки определите, в какой цвет ее нужно покрасить.
Входные данные
Первая строка содержит два целых числа и (, ).
Каждая из следующих строк содержит два целых числа и (, ).
Гарантируется, что никакие две точки не совпадают.
Выходные данные
Выведите строку, состоящую из символов: -й символ строки должен обозначать цвет -й точки.
Для зеленой точки выведите букву G, для синей точки — букву B, а для красной точки — букву R.
Подзадачи
| № | баллы | необх. подзадачи | ограничения |
| 0 | 0 | - | Тесты из условия |
| 1 | 10 | - | , все точки расположены на одной прямой |
| 2 | 15 | 1 | Все точки расположены на одной прямой |
| 3 | 10 | - | , гарантируется, что нет синих точек |
| 4 | 10 | 1, 3 | |
| 5 | 15 | 3 | , гарантируется, что нет синих точек |
| 6 | 15 | 1, 3, 4, 5 | |
| 7 | 5 | - | , все точки являются вершинами строго выпуклого многоугольника и даны в порядке обхода против часовой стрелки |
| 8 | 20 | 1, 2, 3, 4, 5, 6, 7 | Нет доп. огранчений |
| STDIN | STDOUT |
6 4 -1 -1 1 -2 4 -2 2 -4 2 3 -4 -5 | GGBBRG |
2 1 1 1 2 2 | GG |
Примечание
Рассмотрим некоторые точки из первого примера. Точка окрашена в зеленый цвет, потому что можно выбрать точку в качестве следующей, и процесс посетит точку бесконечное количество раз. Данный пример был рассмотрен выше в условии задачи.
Можно показать, что точка не является зеленой, однако она является синей, так как можно выбрать точку 1 в качестве следующей, точка 3 окажется начальной еще хотя бы один раз. Процесс для начальной точки 1 и следующей точки 3 проиллюстрирован на рисунках 5, 6 и 7 ниже.
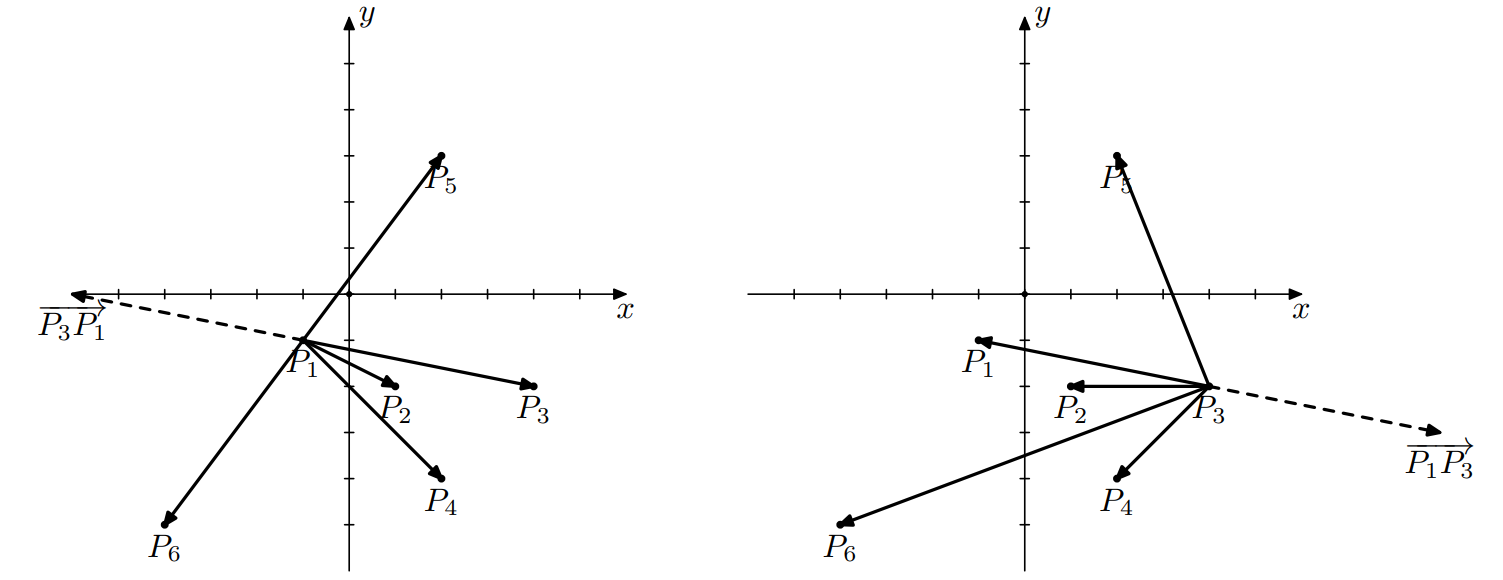
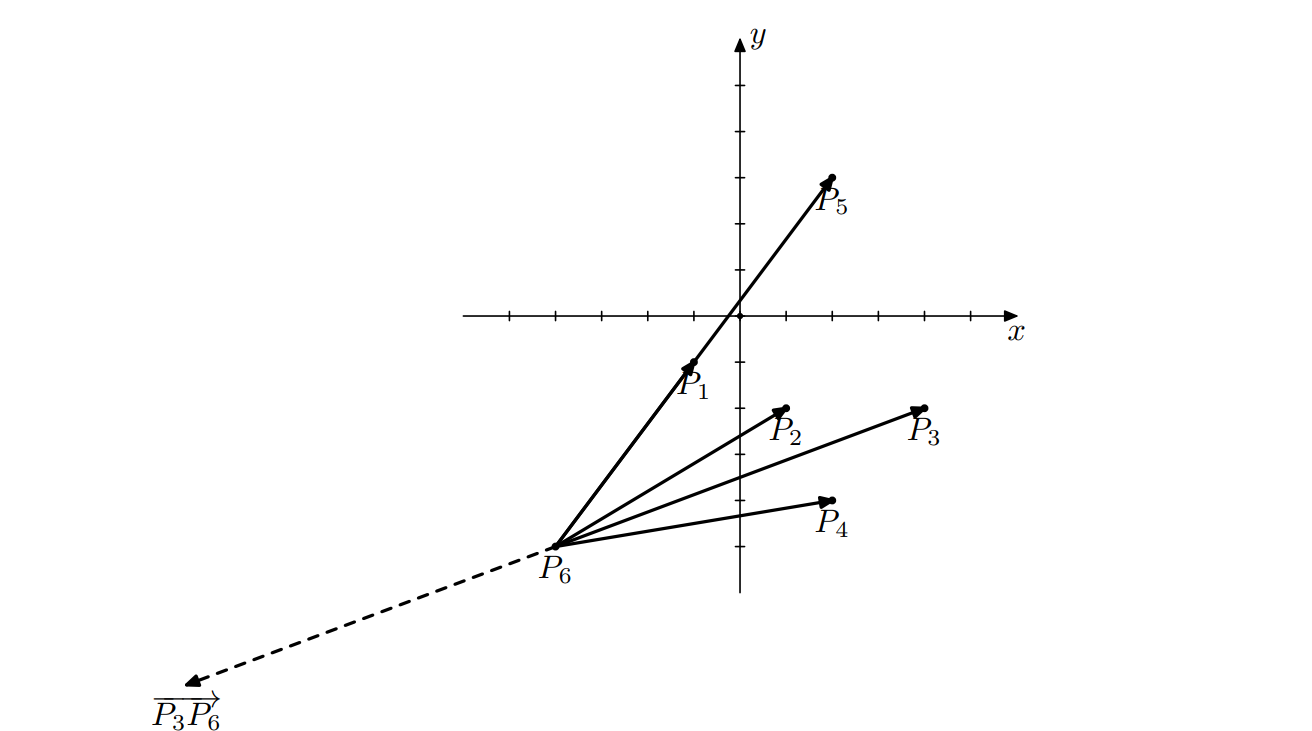
Для начальной точки 3 и следующей точки 1 точки будут упорядочены следующим образом: . Точка с номером 3 становится прицельной. Далее для начальной точки 1 и следующей точки 3 точки будут упорядочены следующим образом: . Точка с номером 6 становится прицельной. Наконец, для начальной точки 3 и следующей точки 6 точки будут упорядочены следующим образом: . Точка с номером 1 становится прицельной. Далее процесс продолжится с начальной точкой 6 и следующей точкой 1. Из примера, описанного выше в условии задачи, мы знаем, что процесс зациклится, посещая точки с номерами 6, 1 и 2.
Рисунок 5: Процесс для начальной точки 3 и следующей точки 1.
Рисунок 6: Процесс для начальной точки 1 и следующей точки 3.
Рисунок 7: Процесс для начальной точки 3 и следующей точки 6.
Во втором примере из условия легко показать, что если одна из точек является начальной, а другая — следующей, то прицельной станет точка, которая являлась начальной. Поэтому обе точки будут окрашены в зеленый цвет.